什么是堆(Heap)?从原理到应用的全面解析
堆是一种特殊的树形数据结构,它满足堆属性:在最大堆中,父节点的值总是大于或等于其子节点的值;在最小堆中,父节点的值总是小于或等于其子节点的值。这种特性使得堆在排序、优先级队列等场景中非常有用。
堆的定义与特性
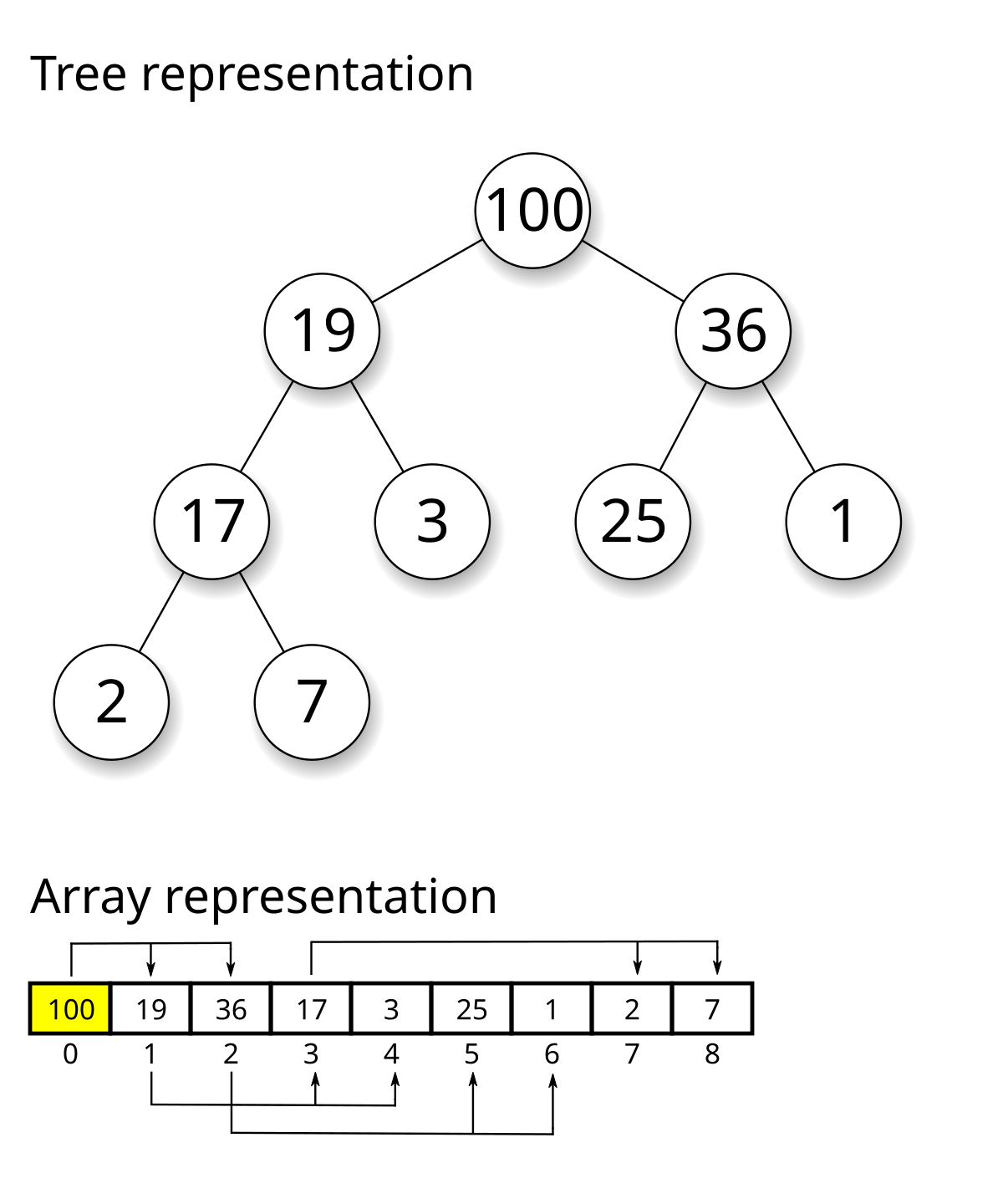
堆是一种基于树的数据结构,通常用完全二叉树表示。 理解堆的关键在于其定义的两种类型:
- 最大堆:对于任何节点 i,其值大于或等于其子节点的值。根节点是堆中的最大值。
- 最小堆:对于任何节点 i,其值小于或等于其子节点的值。根节点是堆中的最小值。
堆的另一个关键特性是其存储方式。虽然逻辑上是树形结构,但堆通常使用数组来存储,这使得定位父节点和子节点非常高效。假设父节点的索引是 i,那么其左子节点的索引是 2i + 1,右子节点的索引是 2i + 2。
堆的基本操作
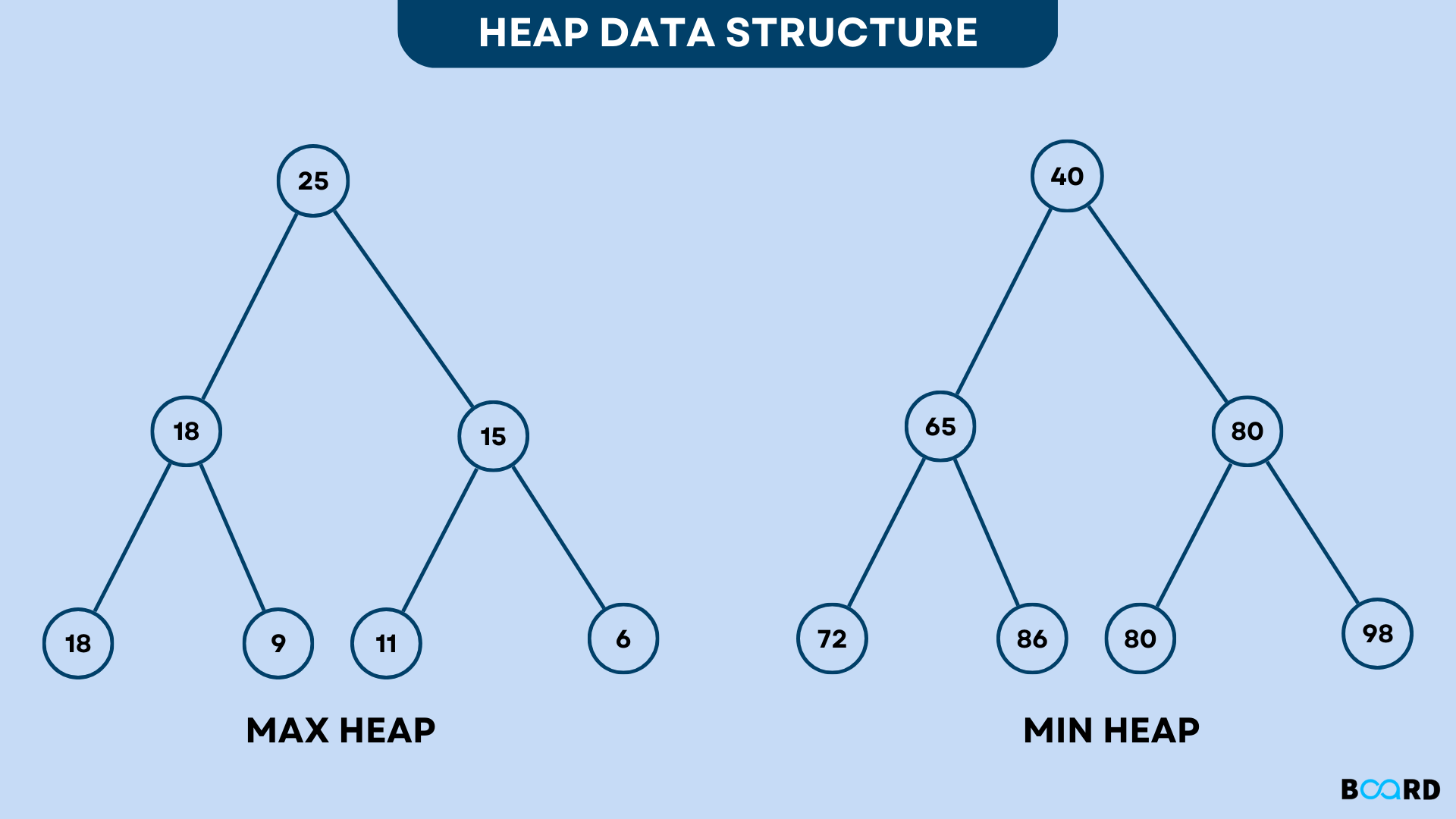
理解堆的操作是掌握其应用的基础,主要包括以下几个核心操作:
插入 (Insert)
在堆中插入一个新元素需要保持堆的属性。通常,新元素会被添加到堆的末尾(数组的最后一个位置),然后通过“上浮”(heapify up)操作,将新元素与其父节点进行比较,如果违反了堆的属性,则交换它们的位置,直到满足堆的属性为止。
删除 (Delete)
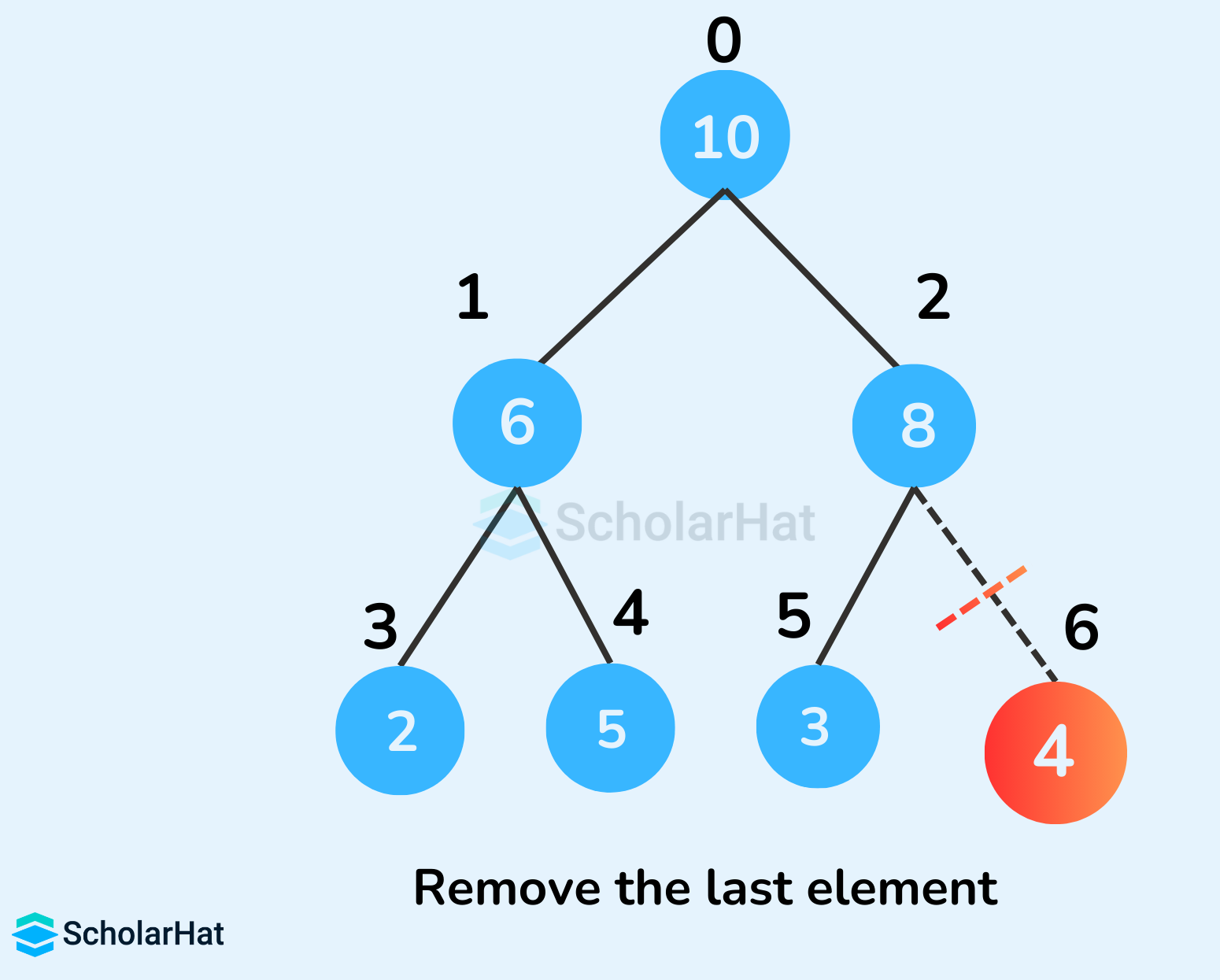
删除操作通常是指删除堆顶元素(最大堆中的最大值或最小堆中的最小值)。删除后,需要将堆的最后一个元素移动到堆顶,然后通过“下沉”(heapify down)操作,将该元素与其子节点进行比较,如果违反了堆的属性,则与子节点中较大(或较小)的那个交换位置,直到满足堆的属性为止。
构建堆 (Build Heap)
构建堆是从一个无序数组创建一个堆的过程。一种常见的方法是从最后一个非叶子节点开始,逐个对每个节点执行“下沉”操作,直到根节点。这个过程的时间复杂度是 O(n)。
堆的实现(Python 示例)
以下是用 Python 实现最大堆的示例代码,演示了插入和删除操作:
import heapqclass MaxHeap: def __init__(self, items=[]): self._heap = [-x for x in items] # 存储负数,模拟最大堆 heapq.heapify(self._heap) def push(self, item): heapq.heappush(self._heap, -item) def pop(self): return -heapq.heappop(self._heap) def peek(self): return -self._heap[0] if self._heap else None def is_empty(self): return not bool(self._heap)# 示例max_heap = MaxHeap([1, 5, 2, 8, 3])print("初始最大堆:", [max_heap.pop() for _ in range(len(max_heap._heap))]) # 输出:[8, 5, 3, 2, 1]max_heap.push(10)max_heap.push(4)print("插入后的最大堆顶:", max_heap.peek()) # 输出:10print("删除堆顶元素:", max_heap.pop()) # 输出:10这段代码使用了 Python 的 `heapq` 模块,该模块默认实现的是最小堆,因此通过存储元素的相反数来模拟最大堆。
堆的应用场景
堆在计算机科学中有着广泛的应用,以下列举几个典型的应用场景:
优先级队列 (Priority Queue)
优先级队列是一种特殊的队列,其中每个元素都有一个优先级。堆非常适合实现优先级队列,因为它可以快速找到队列中优先级最高的元素(最大堆)或优先级最低的元素(最小堆)。
排序 (Heapsort)
堆排序是一种基于堆的排序算法。它的基本思想是首先将数组构建成一个堆,然后重复地将堆顶元素(最大值或最小值)与数组的最后一个元素交换,并重新调整堆,直到所有元素都被排序。堆排序的时间复杂度是 O(n log n),是一种高效的排序算法。
图算法 (Graph Algorithms)
在图算法中,如 Dijkstra 最短路径算法和 Prim 最小生成树算法,堆被用于高效地选择下一个要处理的节点。通过维护一个包含节点和其当前最短距离的最小堆,可以快速找到距离源节点最近的节点。
内存管理 (Memory Management)
在内存管理中,堆可用于跟踪可用内存块。例如,可以使用最小堆来找到最适合分配给定大小的内存块,这有助于减少内存碎片。
堆与其他数据结构的比较
堆和其他数据结构,如数组、链表、二叉搜索树,各有优缺点。理解这些差异有助于在不同场景下选择合适的数据结构。
| 数据结构 | 插入 | 删除最小值/最大值 | 查找最小值/最大值 | 优点 | 缺点 |
|---|---|---|---|---|---|
| 数组 (无序) | O(1) | O(n) | O(n) | 插入快 | 查找/删除慢 |
| 数组 (有序) | O(n) | O(1) | O(1) | 查找快 | 插入慢 |
| 链表 (无序) | O(1) | O(n) | O(n) | 插入快 | 查找/删除慢 |
| 二叉搜索树 | O(log n) (平均) | O(log n) (平均) | O(log n) (平均) | 查找/插入/删除相对快 | 不平衡时性能下降 |
| 堆 | O(log n) | O(log n) | O(1) | 查找最值快,插入/删除适中 | 查找非最值慢 |
高级堆结构
除了基本的二叉堆,还存在一些高级的堆结构,例如:
- 二项堆:二项堆是由一组二项树组成的,支持更快的合并操作。
- 斐波那契堆:斐波那契堆是一种更复杂的数据结构,它在某些操作上具有更好的平均时间复杂度,特别是在 Dijkstra 算法中使用时。
总结
堆是一种功能强大的数据结构,它在排序、优先级队列、图算法等领域有着广泛的应用。通过理解堆的原理、操作和应用场景,可以更好地利用它来解决实际问题。 进一步学习包括研究不同的堆变体及其各自的性能特点。
参考资料:
- 维基百科 - 堆 (数据结构)
- Python heapq 模块官方文档
