深入理解Heap（堆）：概念、应用与实现
Heap（堆）是一种特殊的树状数据结构，它满足堆属性：即树中任意节点的值总是大于（或小于）其子节点的值。堆常被用来实现优先队列，广泛应用于排序算法（如堆排序）、任务调度、内存管理等领域。本文将全面介绍堆的概念、类型、常见操作、实际应用以及如何使用Python实现一个简单的堆。
什么是Heap（堆）？
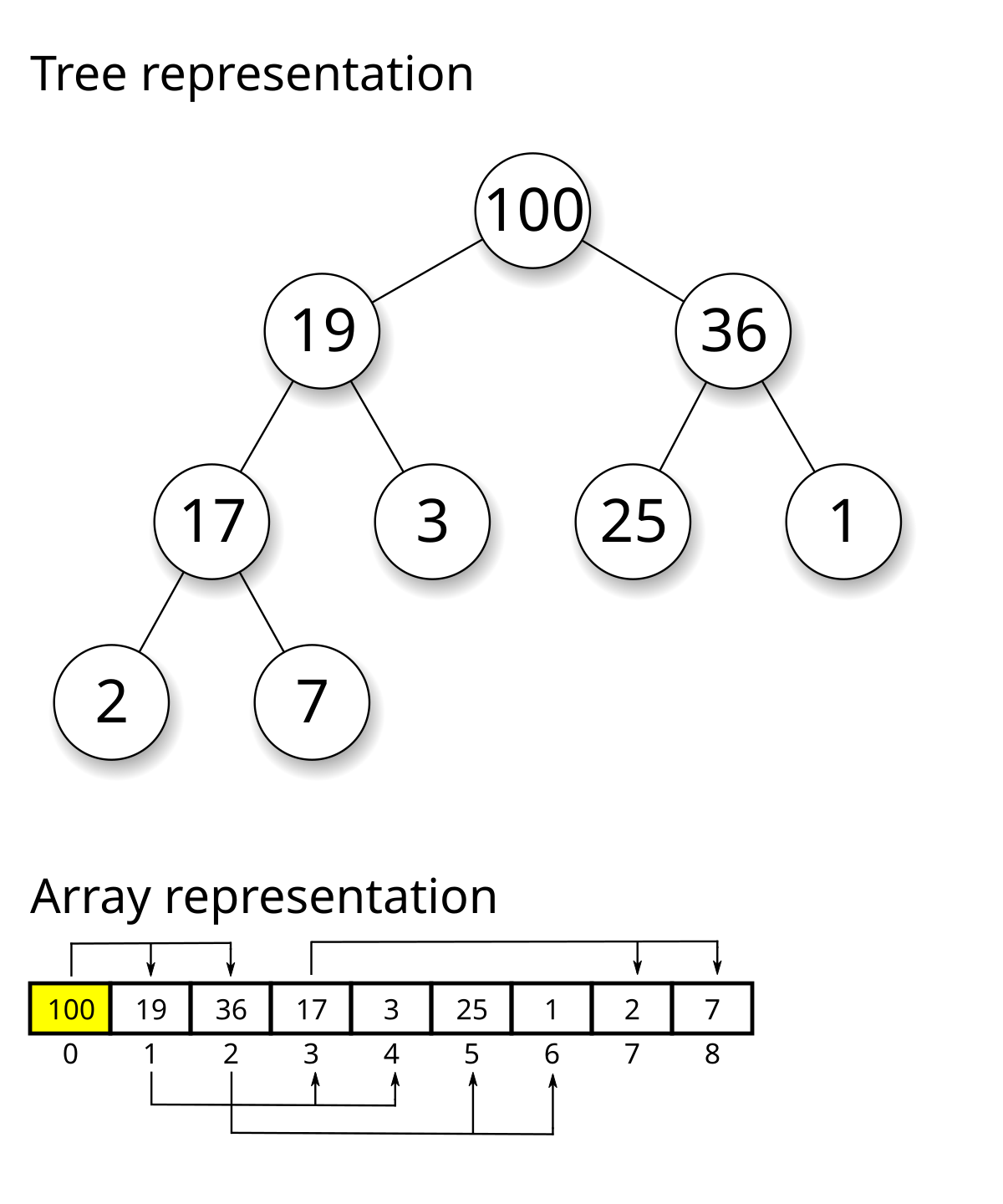
堆是一种特殊的树状数据结构，也是一种基于树的抽象数据类型。它最重要的性质是满足堆属性。根据堆属性的不同，堆可以分为两种主要类型：
最大堆（Max Heap）
在最大堆中，父节点的值总是大于或等于其子节点的值。因此，最大堆的根节点是树中最大的元素。
最小堆（Min Heap）
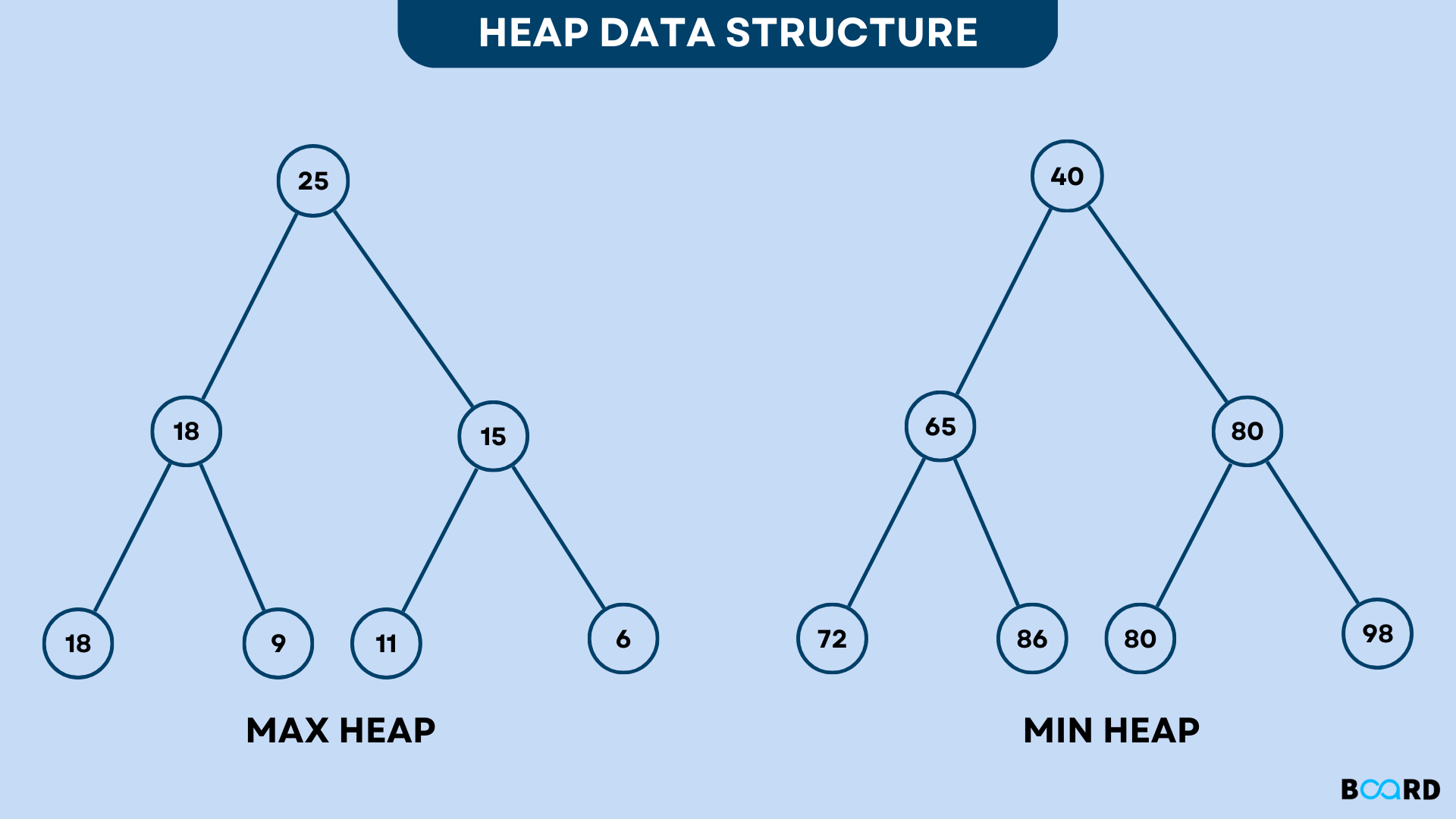
在最小堆中，父节点的值总是小于或等于其子节点的值。因此，最小堆的根节点是树中最小的元素。
堆通常用数组来存储，这使得我们可以很容易地通过索引来访问节点及其父节点、子节点。对于索引为i的节点，其父节点的索引为(i-1)/2，左子节点的索引为2*i+1，右子节点的索引为2*i+2。
Heap（堆）的常见操作
以下是堆的一些常见操作：
插入（Insert）
将一个新元素插入到堆中。为了保持堆属性，通常需要将新元素“上浮”（heapify up）到正确的位置。具体步骤如下：
- 将新元素添加到堆的末尾（数组的最后一个位置）。
- 比较新元素与其父节点的值。
- 如果新元素违反了堆属性（例如，在最大堆中，新元素比父节点大），则交换它们。
- 重复步骤2和3，直到新元素到达正确的位置或成为根节点。
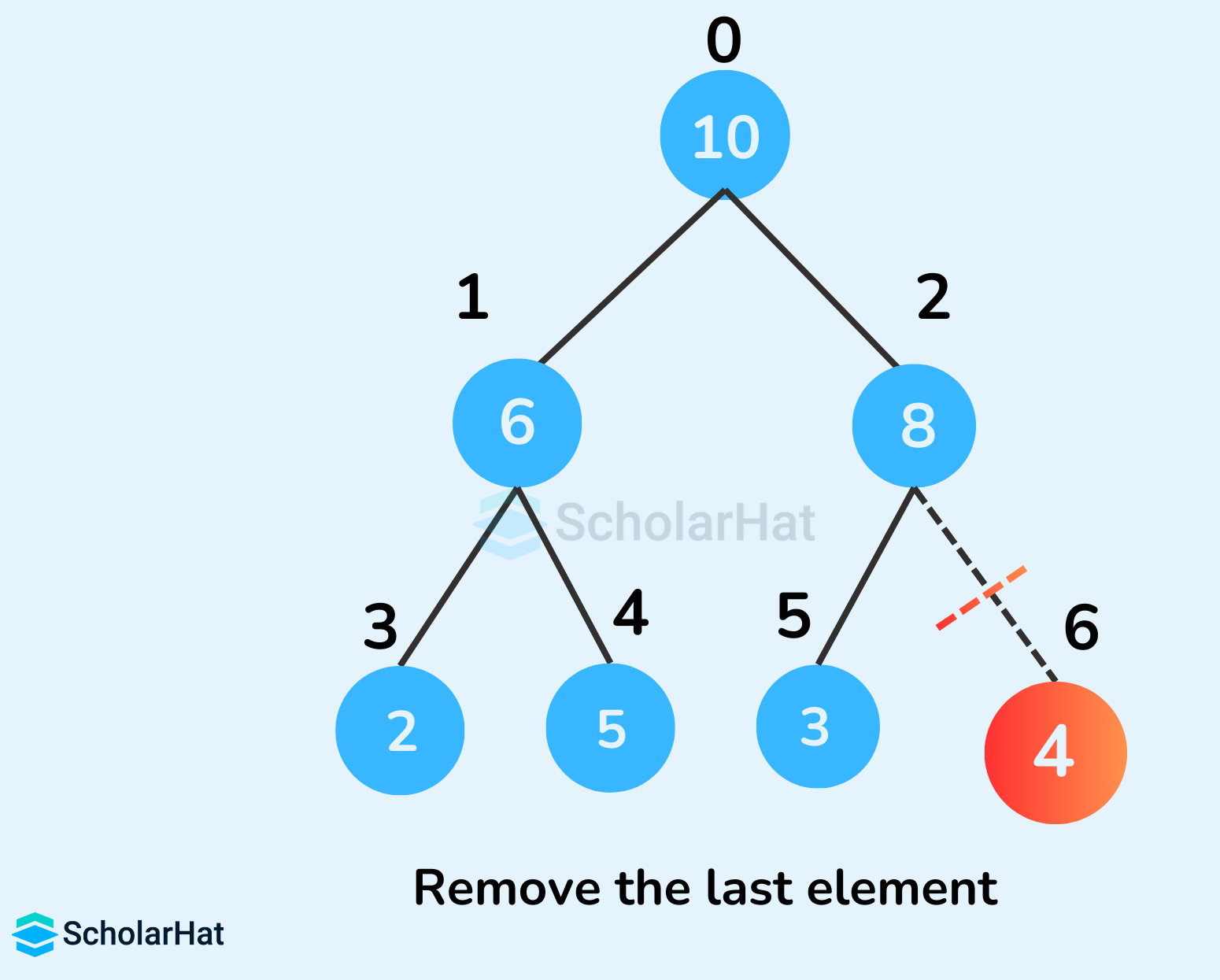
删除（Delete）
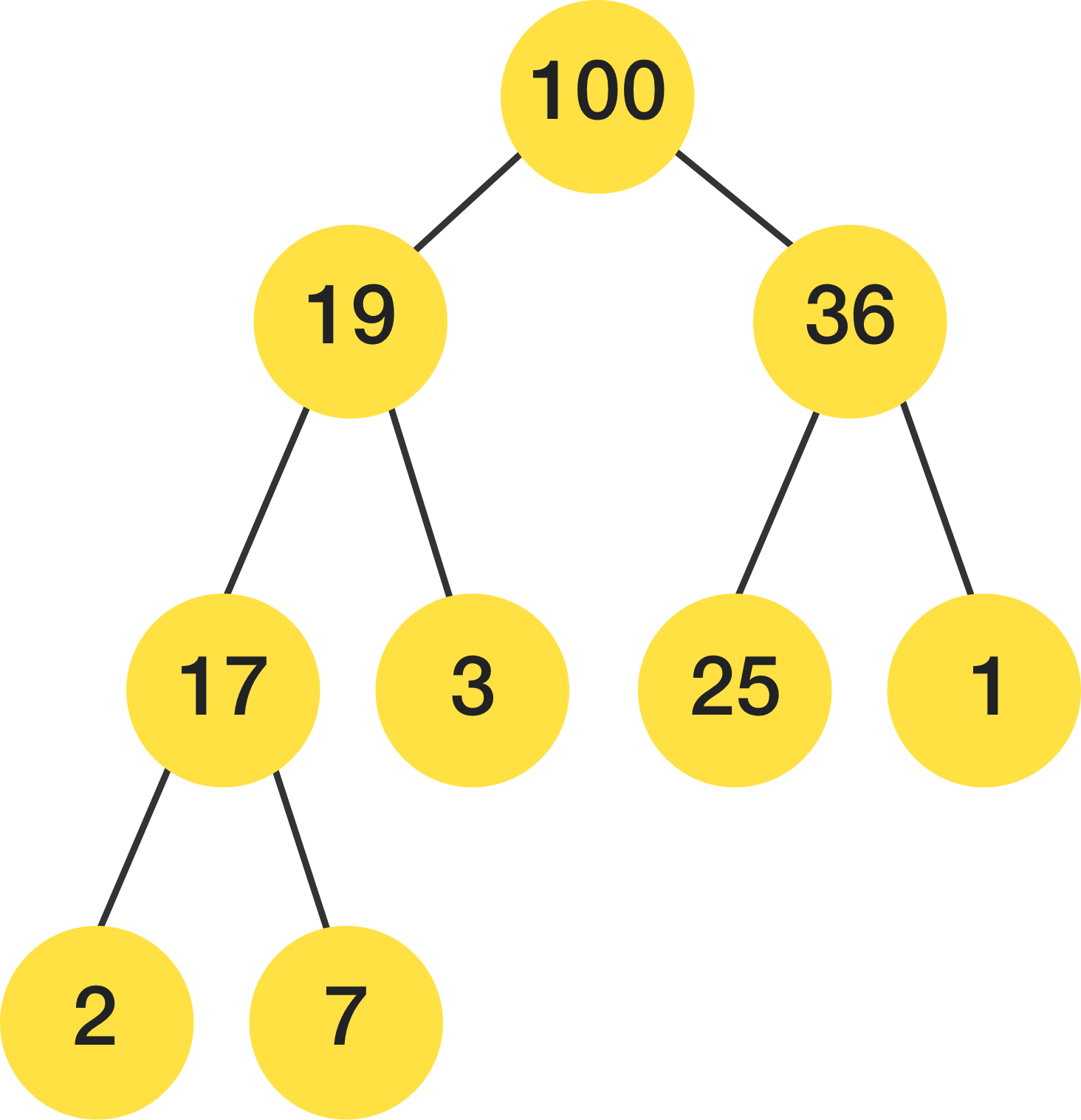
删除堆中的根节点（最大或最小值）。为了保持堆属性，通常需要将最后一个元素移动到根节点，并进行“下沉”（heapify down）操作。具体步骤如下：
- 将最后一个元素移动到根节点的位置。
- 比较根节点与其子节点的值。
- 如果根节点违反了堆属性（例如，在最大堆中，根节点比子节点小），则与较大的子节点交换。
- 重复步骤2和3，直到根节点到达正确的位置或没有子节点。
查找最大/最小值（Find Max/Min）
根据堆的类型，可以直接返回根节点的值。最大堆返回最大值，最小堆返回最小值。
构建Heap（Build Heap）
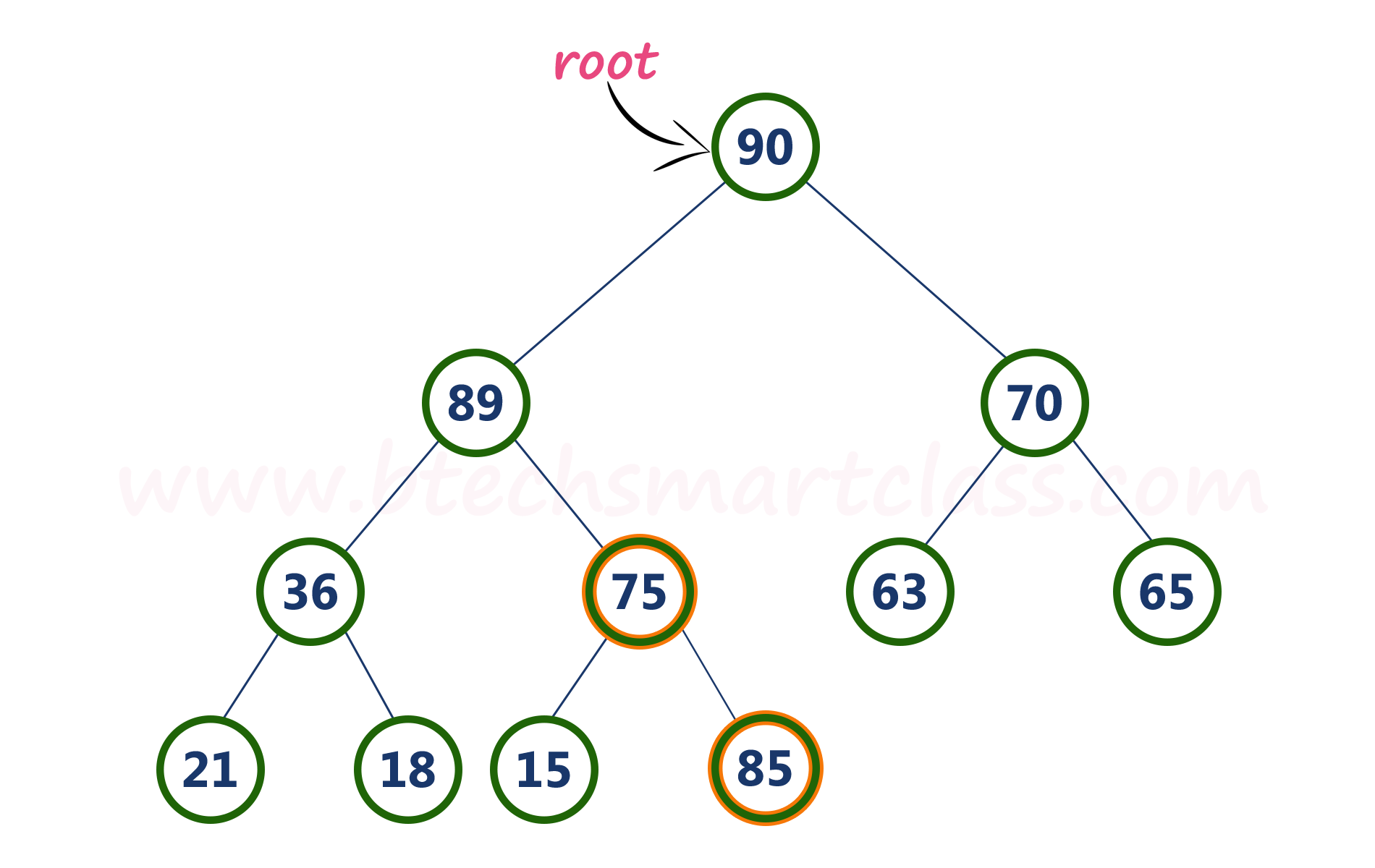
将一个无序的数组构建成一个堆。通常可以使用“自底向上”的方法构建堆，从最后一个非叶子节点开始，依次对每个节点进行“下沉”操作。
Heap（堆）的应用
堆在计算机科学中有着广泛的应用：
优先队列（Priority Queue）
堆最常见的应用是实现优先队列。优先队列是一种抽象数据类型，它允许按照优先级顺序访问元素。堆可以高效地实现优先队列的插入和删除操作，时间复杂度为O(log n)。
Heap（堆）排序（Heap Sort）
堆排序是一种高效的排序算法，时间复杂度为O(n log n)。它首先将待排序的数组构建成一个堆，然后重复删除根节点（最大或最小值），并将其放置到已排序的数组中。
任务调度（Task Scheduling）
在任务调度系统中，可以使用堆来管理任务的优先级。可以根据任务的优先级将其插入到堆中，调度器总是选择堆顶的任务执行。
内存管理（Memory Management）
在内存管理中，可以使用堆来管理空闲内存块的大小。可以根据空闲内存块的大小将其插入到堆中，当需要分配内存时，可以选择堆顶的最小或最大的空闲内存块。
Heap（堆）的Python实现
Python的heapq模块提供了堆的实现。以下是一个使用heapq模块实现最小堆的示例：
pythonimport heapq# 创建一个空列表作为堆heap = []# 插入元素heapq.heappush(heap, 5)heapq.heappush(heap, 1)heapq.heappush(heap, 3)heapq.heappush(heap, 8)print("初始堆:", heap) # 输出: [1, 5, 3, 8]# 获取最小值min_value = heapq.heappop(heap)print("最小值:", min_value) # 输出: 1print("删除最小值后的堆:", heap) # 输出: [3, 5, 8]# 获取当前最小值，但不删除min_value = heap[0]print("当前最小值（不删除）:", min_value) # 输出 3# 将列表转换为堆my_list = [4, 2, 7, 9, 1]heapq.heapify(my_list)print("列表转换为堆:", my_list) # 输出: [1, 2, 7, 9, 4]
Heap（堆）与二叉搜索树（BST）的区别
虽然堆和二叉搜索树（BST）都是树形数据结构，但它们有重要的区别。最主要的区别在于它们的节点排序方式和用途。
| 特性 | Heap（堆） | 二叉搜索树 (BST) |
|---|---|---|
| 排序方式 | 父节点与子节点之间存在大小关系 (最大堆或最小堆)，兄弟节点之间没有明确关系。 | 左子树的所有节点小于根节点，右子树的所有节点大于根节点。 |
| 用途 | 优先队列、堆排序等。 | 查找、插入、删除操作，维护有序数据。 |
| 平衡性 | 通常是完全二叉树，高度相对较低。 | 可能是不平衡的，最坏情况下可能退化为链表。 |
| 查找特定元素 | 不擅长查找特定元素，只能快速找到最大或最小值。 | 适合查找特定元素，平均时间复杂度为 O(log n)。 |
总的来说，堆更适合用于优先队列和堆排序等需要快速访问最大或最小值的场景，而二叉搜索树更适合用于需要频繁进行查找、插入和删除操作，并保持数据有序的场景。
总结
Heap（堆）是一种功能强大的数据结构，它在计算机科学中有着广泛的应用。通过理解堆的概念、类型、常见操作和应用，可以更好地利用堆来解决实际问题。希望本文能够帮助你深入理解堆，并在你的项目中使用它来提高效率。
参考资料：
- Python heapq 模块文档
- Wikipedia: Heap (data structure)