什么是Parabola?深入理解抛物线
Parabola(抛物线)是数学中一种重要的二次曲线,它定义为到定点(焦点)和定直线(准线)距离相等的点的集合。本文将深入浅出地介绍Parabola的定义、性质、方程、应用以及相关概念,帮助你全面理解这一数学概念。
Parabola的定义与基本要素
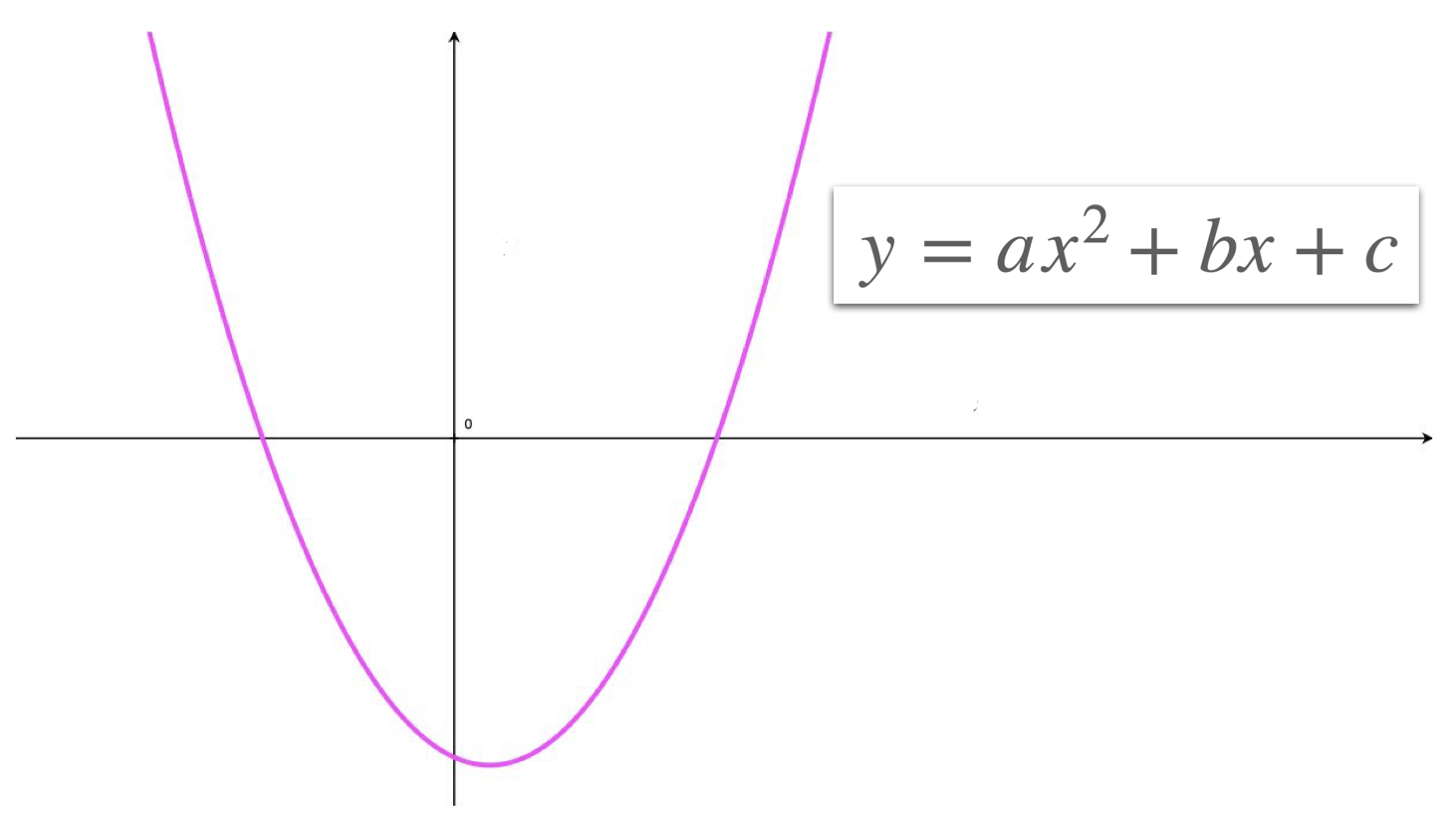
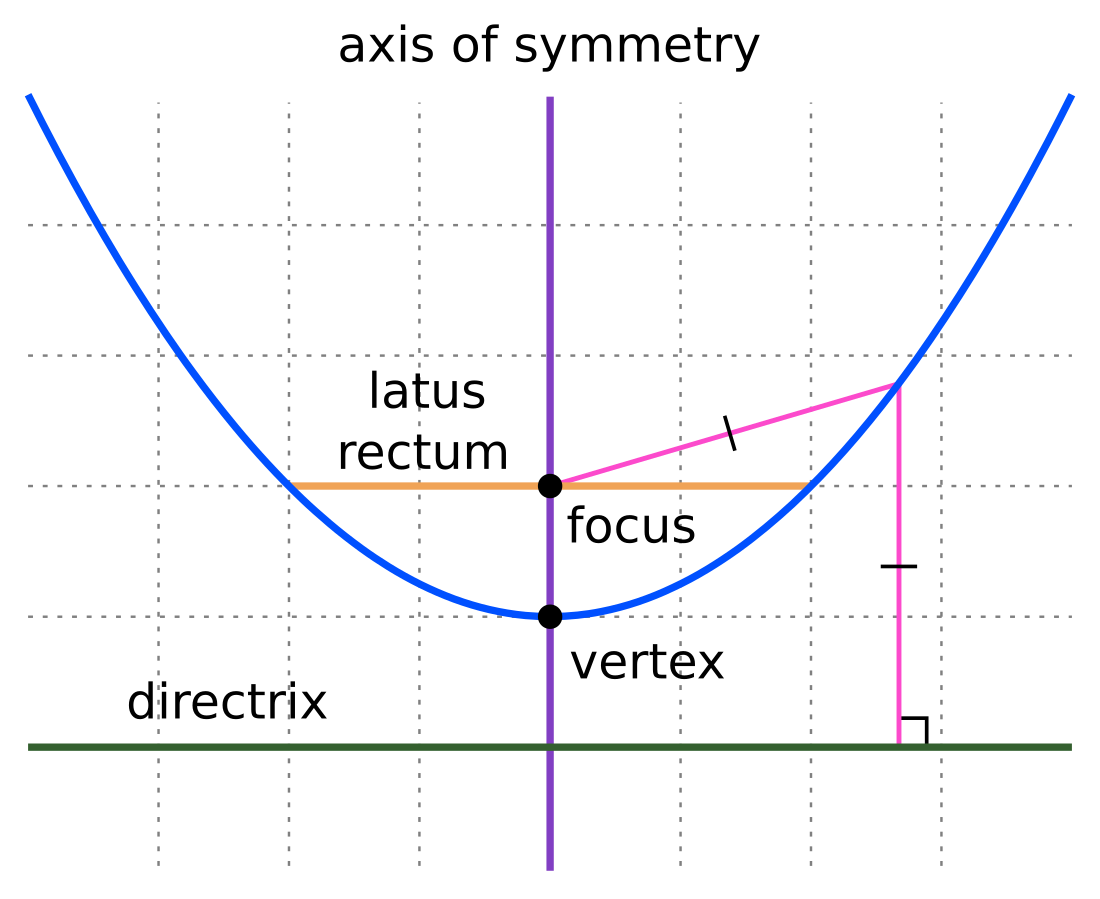
Parabola 是平面内到定点 F(焦点)和定直线 l(准线)距离相等的点的集合。可以用以下公式表达:|PF| = d,其中 |PF| 是点 P 到焦点 F 的距离,d 是点 P 到准线 l 的距离。
Parabola有以下几个关键要素:
- 焦点 (Focus): 定义Parabola的定点,通常用 F 表示。
- 准线 (Directrix): 定义Parabola的定直线,通常用 l 表示。
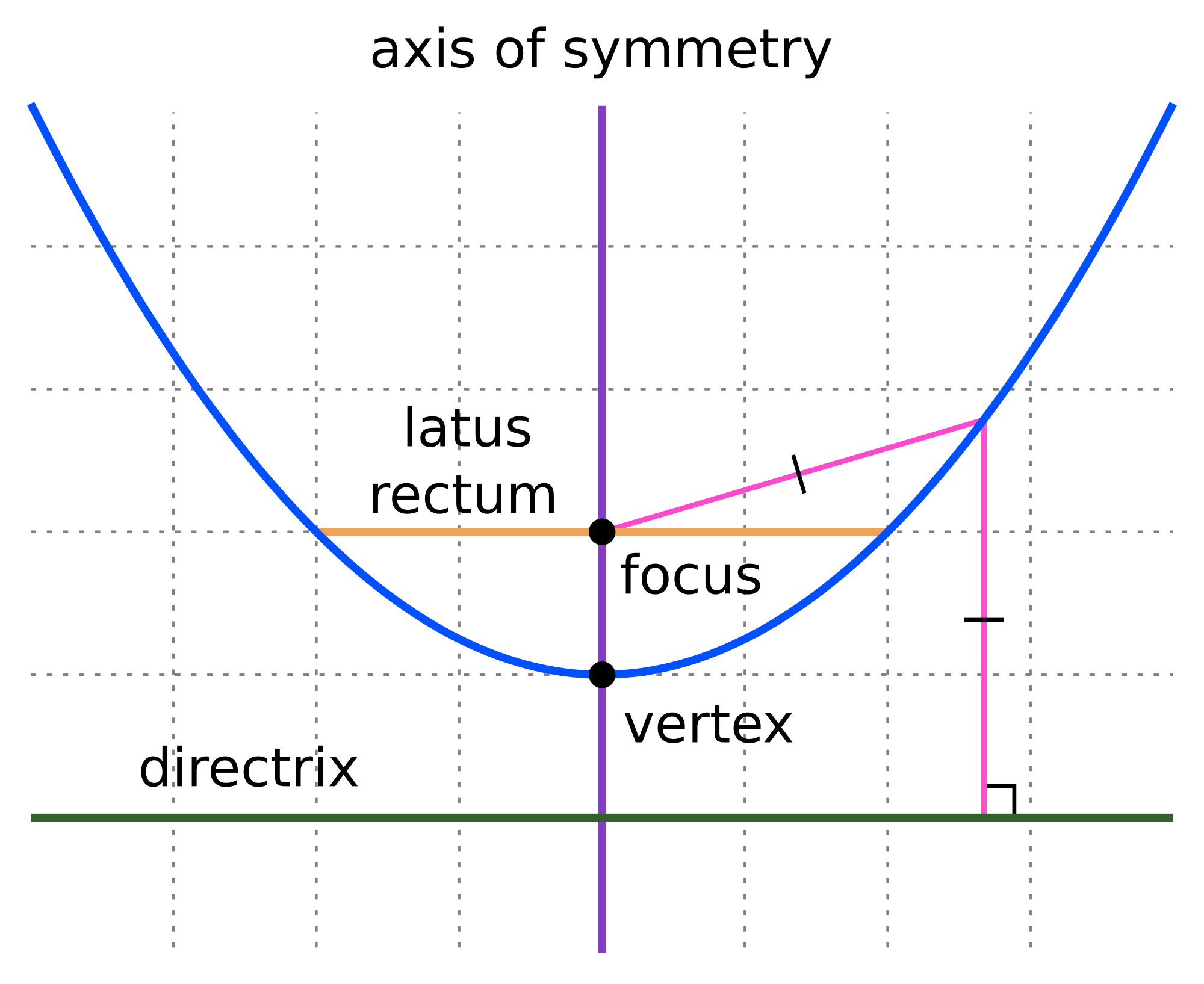
- 顶点 (Vertex): Parabola与其对称轴的交点。顶点是焦点到准线距离的中点。
- 对称轴 (Axis of Symmetry): 通过焦点并垂直于准线的直线。
- 焦距 (Focal Length): 焦点到顶点的距离,通常用 p 表示。焦点到准线的距离为 2p。
Parabola的方程
标准方程
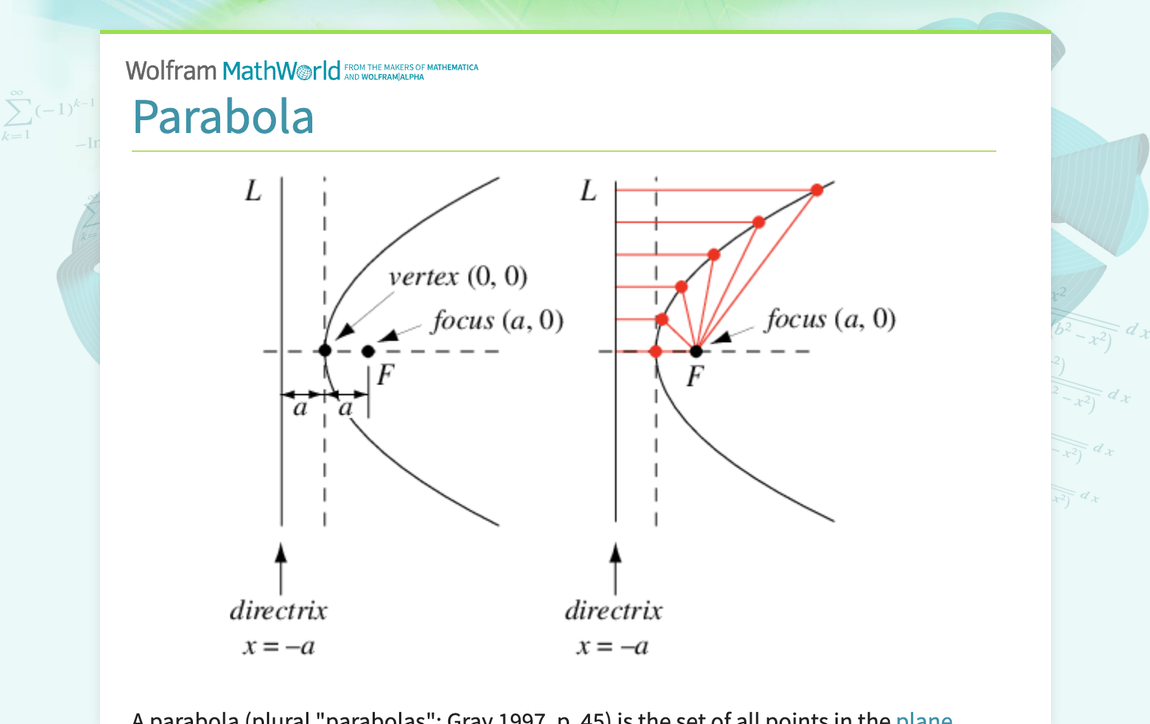
在直角坐标系中,Parabola有几种不同的标准方程,取决于其开口方向和顶点位置。
- 开口向右的Parabola: y2 = 4px (顶点在原点,焦点在 (p, 0))
- 开口向左的Parabola: y2 = -4px (顶点在原点,焦点在 (-p, 0))
- 开口向上的Parabola: x2 = 4py (顶点在原点,焦点在 (0, p))
- 开口向下的Parabola: x2 = -4py (顶点在原点,焦点在 (0, -p))
一般方程
Parabola的一般方程形式为:Ax2 + Bxy + Cy2 + Dx + Ey + F = 0,其中 B2 - 4AC = 0。这意味着对于Parabola,二次项的系数满足特定关系。
Parabola的性质
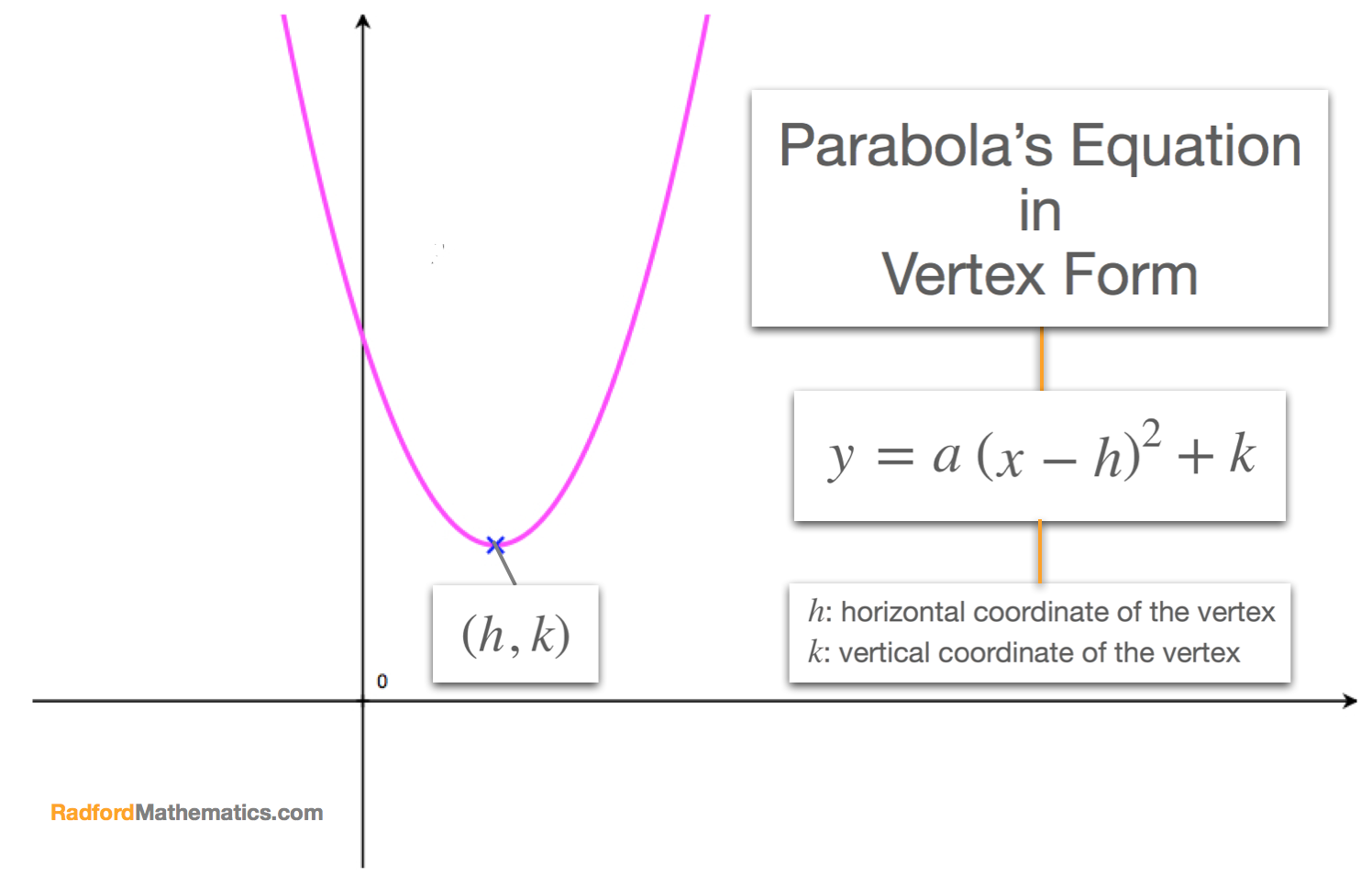
Parabola具有许多独特的几何和物理性质:
- 反射性质: 从焦点发出的光线,经过Parabola反射后,会平行于对称轴射出。反之,平行于对称轴的光线,经过Parabola反射后,会汇聚于焦点。这个性质被广泛应用于太阳能收集器和卫星天线等设备。
- 焦距: 焦距 p 决定了Parabola的开口大小。p 越大,Parabola的开口越大。
Parabola的应用
由于其独特的性质,Parabola在许多领域都有广泛的应用:
- 光学: 太阳能收集器、望远镜、车头灯等都利用了Parabola的反射性质。
- 天文学: 彗星的轨道通常是Parabola或双曲线。
- 建筑学: 拱桥、悬索桥等结构中,Parabola形状可以提供良好的支撑。
- 体育: 篮球、足球等运动的轨迹在一定程度上可以近似为Parabola。
- 无线通信: 卫星天线采用Parabola形状,以集中接收来自卫星的信号。
Parabola的案例分析
案例一:卫星天线
卫星天线是利用Parabola反射性质的典型例子。天线的表面是一个Parabola面,接收来自卫星的微弱信号。这些信号平行于对称轴传播,经过Parabola面反射后,汇聚到焦点位置的接收器上,从而增强信号强度。这种设计使得即使是微弱的卫星信号也能被有效地接收和处理。
案例二:太阳能收集器
太阳能收集器也利用了Parabola的反射性质。太阳光线平行于对称轴照射到Parabola形的反射面上,反射后的光线会汇聚到焦点位置的集热管上,将太阳能转化为热能。这种设计可以有效地提高太阳能的利用率。不同材料的集热管,其集热效率不同。常见集热管的材质及效率参考下表:
| 集热管材质 | 集热效率 | 特点 |
|---|---|---|
| 铜 | 90%-95% | 导热性好,耐腐蚀 |
| 铝 | 85%-90% | 成本较低,重量轻 |
| 不锈钢 | 80%-85% | 强度高,耐高温 |
案例三:抛物线拱桥
一些拱桥的设计采用了Parabola的形状。这种形状可以有效地分散桥梁的重量,并将压力传递到桥墩,从而提高桥梁的稳定性和承载能力。例如,一些历史悠久的石拱桥就采用了这种设计。
总结
Parabola作为一种重要的二次曲线,不仅在数学中具有重要的地位,还在许多实际应用中发挥着关键作用。理解Parabola的定义、性质和方程,可以帮助我们更好地理解和应用相关的技术和设备。通过本文的介绍,相信你对Parabola有了更深入的理解。
参考资料:Wikipedia - Parabola
